02. Intervention, Identification

Intervention in SCM

Intro에서 언급했듯, 만약 내가 A를 바꾼다면 결과 Y가 어떻게 달라질까? 라는 상상을 Intervention이라고 한다. Structural Causal Model(SCM)에서 개입은 아래와 같이 do-operator를 통해 표현된다.

$P(Y|do(T=t))$

즉 $T$를 $t$로 고정할 때(T를 바꿨을 때) $Y$의 확률분포가 어떻게 되는가(결과 Y가 어떻게 달라질까)에 대한 질문을 담고 있다.

$T=t$ 로 고정한다고 하면 Conditioning이랑 조금 비슷해보이기도 한데, 둘은 엄연한 차이가 있다.

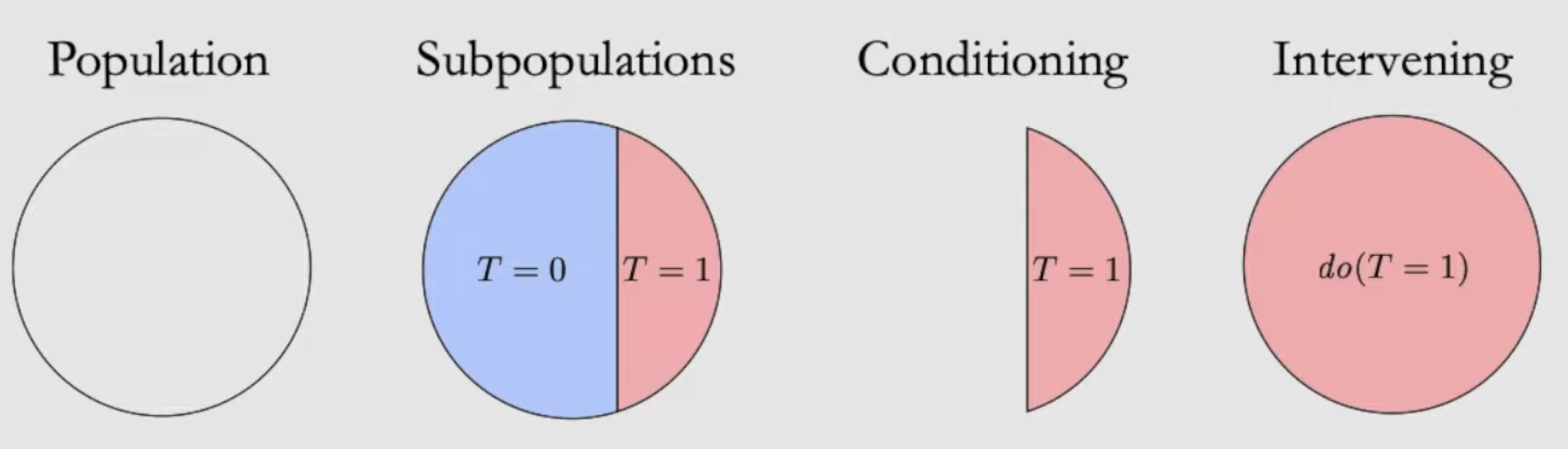
• Conditioning ($P(Y|T=t)$)은 전체 인구 중에서 스스로 처치 $t$를 선택한 사람들의 데이터만 뽑아서 보는 것이다. 즉, 데이터를 특정 부분집합(Subset)으로 제한하는 행위이고,

• 개입(Intervention) $P(Y|do(T=t))$ 은 일부가 아니라, 전체 집단에게 강제로 처치 $t$를 받게 했을 때 어떤 일이 벌어질지 상상하는 것이다.

둘의 차이를 직관적으로 볼 수 있는 그림이 아래에 있다.

그래프적 관점

SCM은 베이지안 네트워크의 성질을 이용한다고 했다. 그래서 그래프와 함께 이해하는 것이 좋은데, intervention을 한다는 것은 해당 변수를 향한 모든 화살표를 제거한다는 의미이기도 하다.

원래 처치($T$)를 결정하던 부모 노드들의 영향력이 내가 개입하는 순간 사라지기 때문이다.

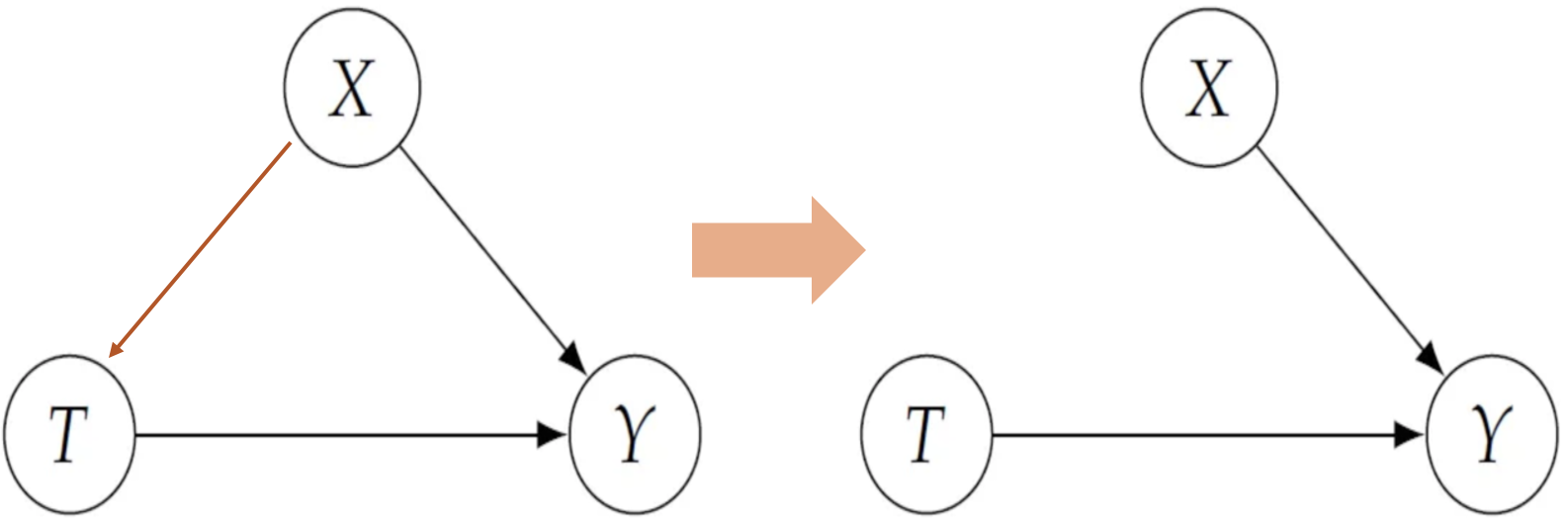
아래 그래프 구조에서, 의사가 원래는 환자의 나이($X$)를 보고 약을 처방할지 말지 결정했다고 하자. 그러면 나이($X$)가 처치 여부($T$)에 영향을 준 것인데(왼쪽 그림),

개입을 하면 나이와 상관없이 전부 약을 처방받는 것이다. 즉 나이($X$)는 더이상 $T$에 영향을 주지 않는다. 화살표가 끊어진다. (오른쪽 그림)

Identification

그런데 수식에 $do(X)$ 연산자가 있는데, 이거는 뭐 어떻게 해야 하는 걸까? 이 연산자는 어떻게 계산해야 할지 감이 오지 않는다. 정의처럼 전체 집단에 강제로 처치를 할 수도 없고,, RCT같은 것이 아니면 저것을 알 수 없는 것은 아닌지 걱정이 생긴다.

그래도 만약 특정 조건을 만족하면, 그래프의 성질을 이용해서 저 $do$ 연산자를 지울 수도 있다! 그래프 성질을 통해 수식을 변형해서 우리가 알고 있는 확률분포로 표현할 수 있다면, 즉 do operator를 제거할 수 있다면, 관측 데이터만으로도 인과효과 추정이 가능하다는 것이다.

이 과정을 Identification(식별)이라고 한다.

Example: Truncated Factorization

우리는 베이지안 네트워크의 성질을 통해 전체 확률 분포를 부모 노드의 조건부확률 곱으로 표현할 수 있다는 것을 안다.

$P(x_1,\dots ,x_n)={\prod }_{i}P(x_i|p{a}_i)$

그리고 아까 Intervention을 한다는 것은 해당 변수를 향한 모든 화살표를 제거한다고도 볼 수 있다고 했다. 즉 $T$에 대한 개입($do(T=t)$)이 있으면, $T$를 결정하던 메커니즘인 $P(t|p{a}_t)$ 항을 식에서 지워버리면 된다. 이를 Truncated Factorization 이라고도 부른다.

아까 예시의 그래프에서 개입이 없는 상태에서의 전체 확률 분포는 다음과 같이 분해할 수 있다.

$P(x,t,y)=P(x)\cdot P(t|x)\cdot P(y|t,x)$

우리가 $T$에 개입하여 강제로 약을 처방한다면($do(T=t)$), 나이($X$)가 약 복용($T$)에 영향을 주던 연결고리 $P(t|x)$가 사라진다. 이때의 분포를 $P_{do(t)}$라고 하면

$P(x,y|do(T=t))=P(x)\cdot 1\cdot P(y|t,x)$

이다.

우리가 최종적으로 알고 싶은 것은 전체 집단에게 약을 먹였을 때의 인과효과(치료율), 즉 $P(y|do(T=t))$인데, 그러면 위 식에서 $X$에 대해 Marginalization을 수행하면 될 것이고, 다음과 같은 결론에 도달한다.

$P(y|do(T=t))={\sum }_{x}P(y|t,x)P(x)$

왼쪽은 do operator가 포함된 식이지만, 오른쪽은 나이별 치료율과 나이의 분포 만으로도 계산할 수 있는 값이다. 이처럼 그래프 구조를 알고 있고 특정 조건을 만족한다면, 실험 없이 관측 데이터만으로도 인과효과에 대한 질문에 답할 수 있다. (그래프 구조가 불분명하거나 측정되지 않은 교란 변수(unmeasured confounder)가 있다면 식별이 불가능할 수도 있다)

위 예시는 backdoor adjustment의 특수한 경우이기도 한데, 이는 다음에 살펴보도록 하자.

---

참고 자료: https://www.bradyneal.com/causal-inference-course