Statistical Model과 Causal Model의 차이
통계 수업을 듣거나 관련 책을 읽다 보면 상관관계는 인과관계가 아니라는 말을 많이 듣게 된다.
자주 나오는 예시가 익사사고와 아이스크림 판매량일 텐데, 데이터를 살펴보면 익사사고의 수와 아이스크림의 판매량이 높은 상관관계를 가지고 있다는 것이다.
하지만 우리는 그렇다고 해서 아이스크림 판매량을 줄이면 익사사고도 줄겠다! 라고 판단하지는 않는다.
보통 이 현상은 익사사고와 아이스크림 판매량이 서로 인과관계가 있는 것이 아니라, 온도, 또는 날씨라는 공통된 원인이 둘에 영향을 미치고 있기 때문이라고 해석한다.
일반적으로도 상관관계가 인과관계를 보장해주지 않는 경우가 매우매우 많다. 그래서 우리는 상관관계를 발견했다고 해서, 곧바로 인과관계로 해석하는 것은 주의해야 한다.
이렇게 상관관계 인과관계를 주의해야 한다고는 쉽게 인식할 수 있지만,,
당장 회귀분석만 하더라도 모델링 후에 A라는 요소를 몇 만큼 늘리면 결과가 어떠어떠하게 달라질 것이다~ 라고 해석하는 경우가 많다. 이 역시 조심해야 한다는 것이다.
통계학에서는 보통 확률 모델을 세우고, 그 모델을 통해 관측된 데이터의 패턴을 설명한다. 반면 인과 모델은 단순히 확률 모델을 포함할 뿐만 아니라, 그보다 더 많은 정보(데이터가 어떻게 생성되는지에 관한)를 담고 있다.
-
확률적 추론(probabilistic reasoning): 주어진 확률 모델로부터 결과를 예측
예: 흡연자 비율이 높은 곳에서는 폐암 발생률이 높을까? A값이 32이면 Y값은 얼마일까?
-
인과적 추론(causal reasoning): 인과 모델을 통해 개입이나 환경 변화의 효과를 분석
예: 흡연을 줄이는 정책을 도입하면 실제로 폐암 발생률이 줄어들까? A값을 1 늘리면 Y값은 어떻게 변화할까?
인과 모델(인과추론)이 필요한 이유
방금
“A라는 요소를 몇 만큼 늘리면 결과가 어떠어떠하게 달라질 것이다.”
라고 했다.
이런 식의 해석은, 만약 내가 A를 조작한다면 결과 Y가 어떻게 달라질까? 라는 상상을 포함한다. 이런 상상을 개입(intervention)이라고 부른다.
이것이 통계 모델과 인과 모델의 차이, 또 인과 모델이 필요한 이유를 잘 나타낸다고 해도 좋을 것 같다. 단순히 예측을 넘어 개입 상황을 알기 위해서는, 즉 개입 분포를 알기 위해서는 인과 모델링이 필요하다!!
예시
유전자의 활성화 수준(Activity) 데이터와 이에 대응하는 표현형(Phenotype) 측정값들을 가지고 있다고 가정해보자. 아래의 그림과 같다.
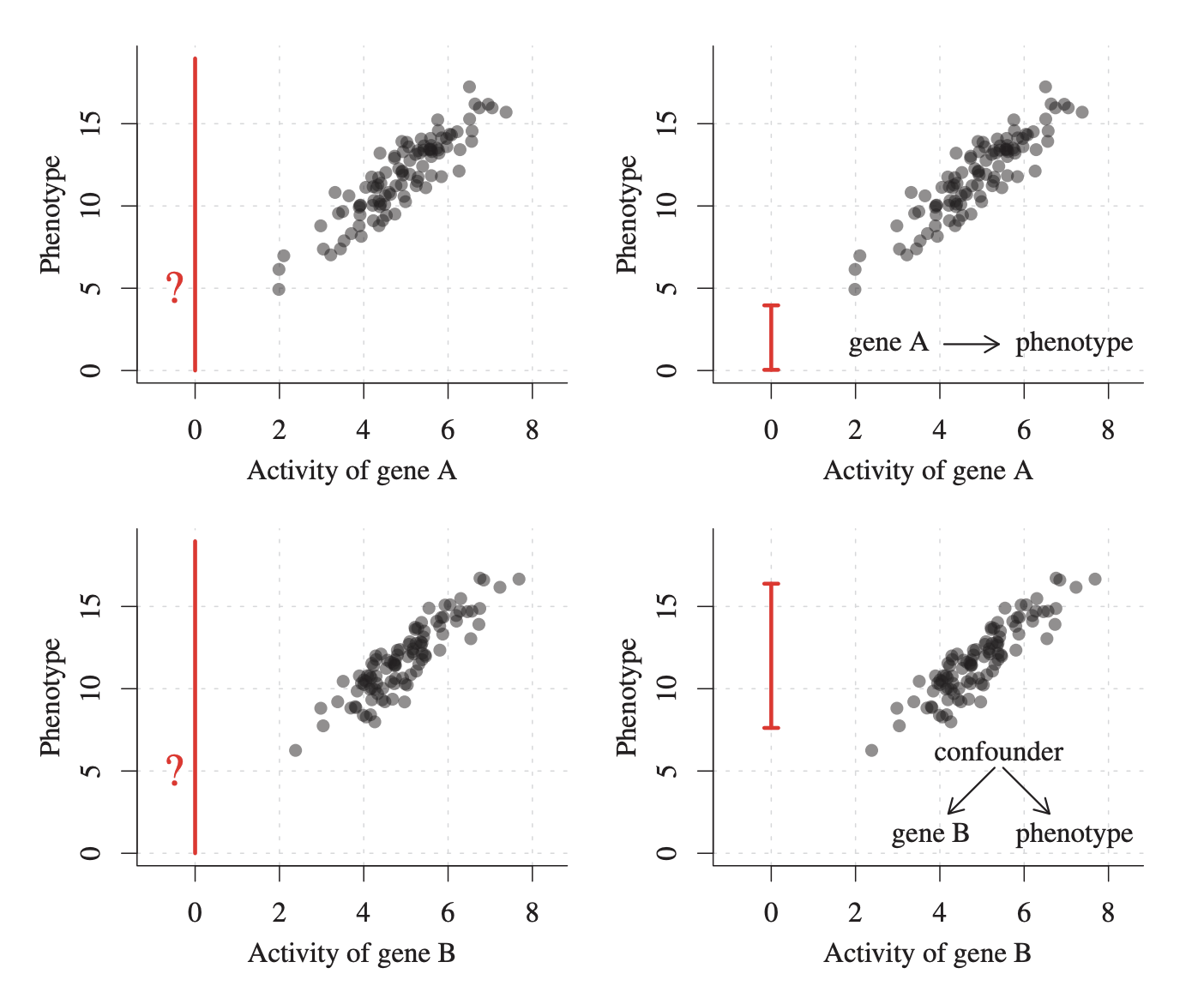
그리고 A와 B는 각각 다른 구조를 가지고 있다고 생각해보자.
- A는 유전자 표현형(phenotype)에 직접적인 영향을 미친다.
- B는 유전자 표현형에 직접적인 영향을 미치지 않는다. 제3의 유전자가 B와 표현형에 동시에 영향을 미친다(여름철 익사사고 수와 아이스크림 판매량처럼)
그래프만 봤을 때 A, B와 phenotype은 확실히 강한 상관 관계가 있다고 할 수 있다. 즉, 유전자 활성도 값을 알면 표현형의 값을 예측할 수 있을 것이다. 예를 들어서, 유전자 A의 활성 값이 6 근처라면, 표현형이 12에서 16 사이일 가능성이 높다.
하지만 우리는,
유전자 A나 B의 활성도를 0으로 설정하면 표현형은 어떻게 될까?
와 같은 개입 상황을 예측하고 싶을 수도 있다.
여기서 단순히 위에서 적용했던 통계적 예측을 이용해서 답을 하는 건 위험하다. 그러나 A와 B, 그리고 유전자 표현형 데이터가 어떻게 생성되었는지 정보를 반영한다면
-
유전자 A는 표현형에 인과적 영향을 주기 때문에
A의 활성도를 0으로 설정했을 때엔 표현형에 변화가 일어난다고 예상할 수 있다. phenotype은 아마 0에서 5 사이일 가능성이 높다. (그림 오른쪽 위)
-
반면 유전자 B와 표현형 간의 상관은 제3의 유전자 같은 공통 원인 때문이므로
유전자 B를 조작해도 표현형에는 아무런 영향이 없다. 아마 여전히 7에서 16 사이일 것이다. (그림 오른쪽 아래).
이 차이는 단순히 결합확률분포나 통계적 모델링 같은 확률적 설명으로는 불가하다. 가 어떻게 생성되었는지에 대한 구조적 정보(그래프 구조, 함수, 노이즈 변수 등)를 포함해야만 논의할 수 있는 것이다.
물론 단순히 데이터가 주어진 상황에서 예측만 하고 싶을 때는 인과 모델이 필요하지 않다.
예를 들어
- 다음 달에 우리 서비스에서 탈퇴할 고객이 몇 명일까?
- 크리스마스에 얼마나 많은 장난감을 준비해야 할까?
와 같은 단순 예측만으로도 충분한 경우는 통계적 모델만으로 충분할 수 있다.
목적에 따라 내가 필요한 모델을 충분히 인지하고 선택적으로 적용할 수 있다면 좋을 것 같다 😆
참고자료: Elements of Causal Inference - Foundations and Learning Algorithms