인과추론의 가정 - 1

ITE, ATE를 보고 오시면 더욱 좋습니다.

이전 장에서, 단순히 관측 데이터만을 비교한 Association Difference와 ATE는 다름을 알아보았다. 수식으로 표현하면 아래와 같다.

$E[Y(1)-Y(0)]=E[Y(1)]-E[Y(0)]\ne E[Y|T=1]-E[Y|T=0]$

그런데 특정 상황에선 Association Difference와 ATE가 같아질 수 있지 않을까? 만약 그 상황을 알 수 있다면 인과 효과를 추정하기가 쉬워질 것 같다.

Ignorability / Exchangeability

그 조건을 Ignorability, 또는 Exchangeability라고 한다. formal하게 정리하면 다음과 같다.

$\text{Ignorbility/Exchangeability : }(Y(1),Y(0))\perp T$

즉 $T$와 Potential Outcome은 독립이라는 건데, 무엇을 의미할까? 공부할 땐 수식으로 보니 좀 더 와닿았기 때문에, 수식을 먼저 보고 시작하자.

$E[Y(1)|T=1]=E[Y(1)|T=0],E[Y(0)|T=1]=E[Y(0)|T=0]$

즉 이전의 두통 예시에서, 환자가 처방을 받았든 받지 않았든 약을 먹거나 먹지 않은 후의 결과는 동일했을 것이라는 의미다.

괴짜 의사 예시에서, 의사는 환자의 상태를 보고 금방 나을 것 같은 환자에게만 약을 주었었다. 이럴 경우 약을 받은 환자가 두통이 낫는 비율이 당연하게도 더 높다.

그런데 이번엔 이 괴짜 의사가 어떤 규제에 의해 온라인으로만 약을 처방해주기로 했다고 생각해보자. 그러면 의사는 환자의 상태를 잘 알아볼 수 없을 테고, 약을 처방 받고, 받지 못한 그룹이 비슷비슷할 것이다. 이는 곧 공변량 $X$(환자의 상태 또는 진단 결과)가 더 이상 약의 처방 여부인 $T$에 영향을 주지 못함을 의미한다. 이를 그래프로 나타내면 아래와 같다.

(여기서 $T$와 $Y$에 Confounding하는 요소가 더이상 없음이 핵심이다.)

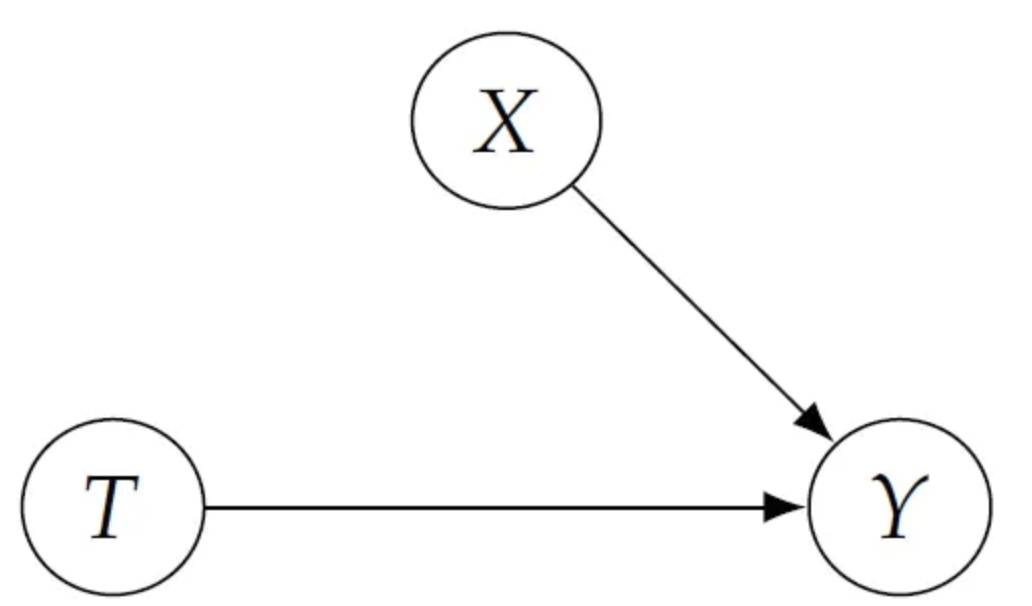
(그래프는 이후에 조금 더 자세히 다룰 예정)

이제 이 $X$는 약의 효과를 측정하는데 무시 가능하다(Ignorable). 또, 약을 받은 그룹과 받지 않은 그룹이 비슷비슷하기 때문에, 만약 약을 받은 그룹이 약을 받지 않고 받지 않은 그룹이 약을 받았어도(Exchange) 약( $T$) 효과의 차이가 같았을 것임을 의미한다.

이러한 조건 하에서는 약의 인과적 효과를 관측 데이터로 계산해도 아래와 같이 제대로 측정할 수 있다. 이처럼 관측 데이터로부터 인과 효과를 계산할 수 있을 때 Causal Effect를 Identifiable하다고 한다.

$$\begin{gathered} \underset{\text{Causal quantity}}{\underbrace{E[Y(1)]-E[Y(0)]}}=E[Y(1)|T=1]-E[Y(0)|T=0] \\ =\underset{\text{Statistical quantity}}{\underbrace{E[Y|T=1]-E[Y|T=0]}} \end{gathered}$$

Randomized Control Trial

그러나 위 가정은 사실 성립하기가 매우 힘들다는 것을 알 수 있다. 만약 의사가 이 약은 젊은 사람들만 복용할 수 있다고 하면서 젊은 사람들 위주로 약을 처방했다면? 아니면 이 의사가 정말정말 감이 좋아서 온라인으로도 금방 나을 것 같은 환자를 잘 구분할 수 있었다면? 아무리 노력을 해도, 처치를 받은 그룹과 받지 않은 그룹이 같다는 것은 불가능할지도 모른다.

그러나 다행히도 Randomized Control Trial(RCT)이 이를 해결해줄 수 있다. 동전을 던져서 앞면이 나오면 약을 처방해주고, 뒷면이 나오면 약을 처방해주지 않는 식으로 실험을 하는 것이다. 이렇게 되면 치료군과 대조군이 연령, 성별, 기저 질환 등 영향을 줄 수 있는 모든 요인에 대해 Exchangeable해지게 된다.

Unconfoundness (Conditional Exchangeability)

그러면 이미 관측된 데이터로부터는 인과 효과의 추정이 불가능할까? RCT로 실험을 다시 해야 하나? 만약에 실험이 비용이나 윤리적인 이유로 불가능한 상황이라면 희망이 없는 걸까?

이때 좀 더 완화된 가정이 우리를 구원해주는데, 바로 Conditional Exchangeability이다.

$\text{Conditional Exchangeability / Unconfoundness : }(Y(1),Y(0))\perp T|X$

약의 처방($T$)와 두통 개선($Y$)에 모두 영향을 주는 ‘나이’라는 변수 $X$가 있다고 해보자. (젊은 사람 위주로 처방해주는 괴짜 의사를 생각해보자) $X$의 존재로 인해 우리는 치료군과 대조군이 Exchangeable하지 않았고, 단순히 평균을 단순 비교해서는 인과 효과를 제대로 추정할 수 없었다. 그런데 만약 같은 나이대로 분류한 다음 치료군과 대조군을 비교한다면?

그러니깐 20대 중에서도 처방을 받지 않은 사람이 있고, 5-60대 중에서도 처방을 받은 사람이 있는 상황을 가정해보자. 그러면 20대에서 처방 받은 사람의 결과와 20대에서 처방 받지 않은 사람의 결과를 비교하면, 적어도 그 해당 비교에서는 나이가 중요한 요소는 아닐 것이다.

이걸 이용해서, 같은 나이($X$)를 가진 사람들끼리만 sub-group으로 나눠서 약의 효과를 비교하면 (어떻게 보면 필터를 추가한 것) 특정 X 하에서의 ATE, Conditional Average Treatment Effect (CATE) 를 구할 수 있다.

$$\begin{gathered} E[Y(1)-Y(0)|X]=E[Y(1)|T=1,X]-E[Y(0)|T=0,X] \\ =E[Y|T=1,X]-E[Y|T=0,X] \end{gathered}$$

이렇게 구한 CATE를 이용해 다시 모든 X에 대한 기댓값을 취하면(marginalizing over X, Law of expected iteration도 참고하면 좋을 듯), 그것이 우리가 구하고자 하는 Causal Effect인 ATE가 될 수 있다. 이는 중요한 인과추론에서 중요한 개념이므로 Adjustment Formula라는 이름을 따로 붙이기로 한다.

Adjustment Formula

Unconfoundedness, Positivity, No interference, Consistency 가정 하에서, ATE를 관측 데이터로부터 구할 수 있다.

$$\begin{array}{r}E[Y(1)-Y(0)]=E_X[E[Y|T=1,X]-E[Y|T=0,X]]\end{array}$$

위 계산 결과를 아직 증명은 하지 않았다. 방금 정리에서 언급된 Unconfoundness 외에 3가지 가정을 자세히 다룬 후에, 이를 증명하기로 한다.

※ 이제 인과 효과를 마음껏 추정할 수 있을 것 같지만, 교란 변수가 W처럼 측정하기 힘든 변수일 수도, 우리가 존재조차 알지 못했던 변수일 수도 있다. 즉 Unconfoundness 역시 만족하기는 쉽지 않다.

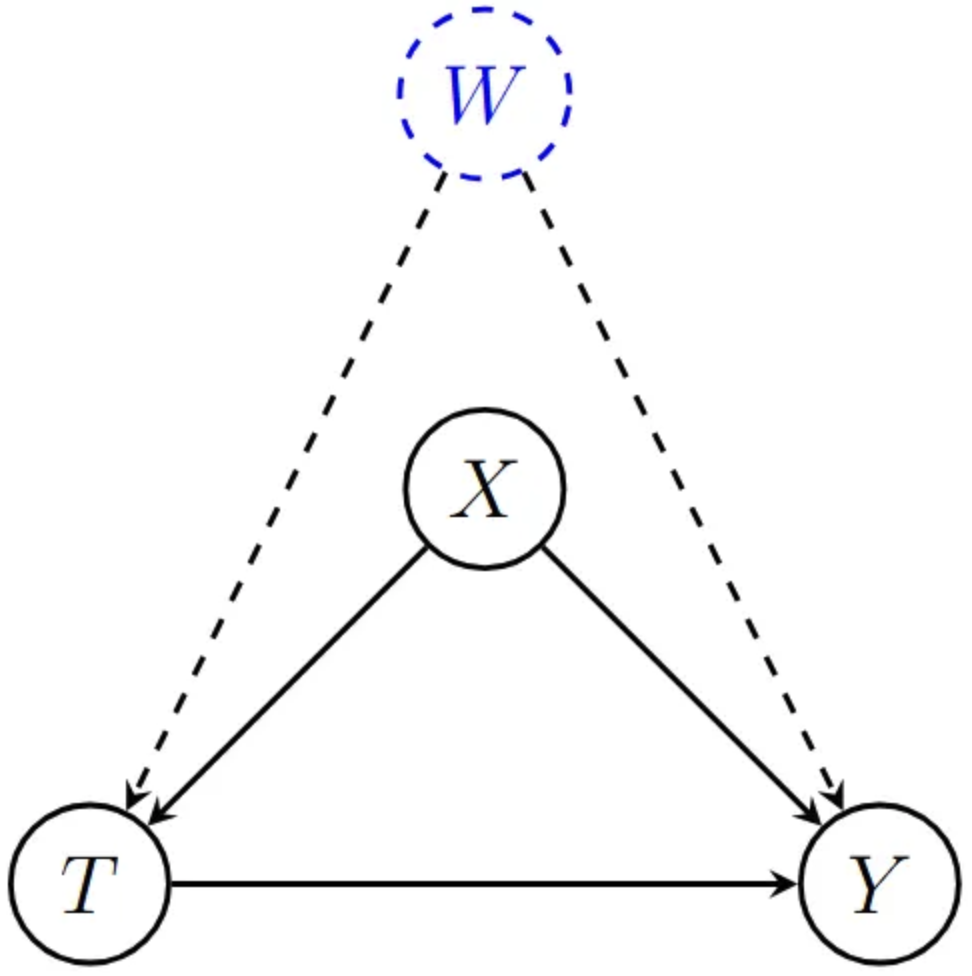
그래도 기존의 Exchangeability에 비해서 정말정말 완화된 조건임은 분명해보인다 ㅎ