Bayesian Network
SCM은 Bayesian Network의 성질을 이용하기 때문에, Bayesian Network를 먼저 이해하고 들어가면 좋다.
※ 참고: 관련 용어들
DAG(Directed Acyclic Graph)란
- Directed : 엣지에 방향성이 있다는 뜻, 화살표가 있으면 Directed, 없으면 Undirected
- Acyclic : Cyclic 의 반대말로, 순환이 없다는 뜻. 한 노드에서 화살표를 타고 따라가면, 다시 돌아오는 길이 없어야 한다.
즉, 순환이 없고 모든 엣지에 방향성이 표현된 그래프
등장할 그래프 관련 용어
- Parent: 특정 노드로 직접 화살표가 향하는 노드 (한 다리만 건넘)
- Child: 특정 노드에서 직접 화살표가 향하는 노드 (한 다리만 건넘)
- Ancestor: 특정 노드로 화살표를 따라 경로 상에서 도달할 수 있는 모든 노드
- Descendant: 특정 노드에서 화살표를 따라 경로 상에서 도달할 수 있는 모든 노드
모두 없을 수도, 있을 수도 있고, 또 여러 개 있을 수도 있다.
만약 우리가 변수 사이의 연관성, 또는 결합확률분포에 관심이 있다고 해보자. 그러면 우선 생각할 수 있는 것은 table 형식으로 그 관계를 표현하는 것이다.
확률의 Factorization에 따라, 로 나타낼 수 있다.
그런데, 이진 변수 4개가 있는 상황을 생각해보자. 그러면 당장 을 표현하는 데에만 개의 파라미터가 필요하다. 만약 변수 각각이 값을 4개 가질 수 있다거나, 변수 하나만 늘어나도 계산해야 할 파라미터는 폭발적(exponentially)으로 늘어난다. 데이터가 그 수보다 작다면, 각 확률을 계산할 수 없다는 문제도 덤으로 발생한다.
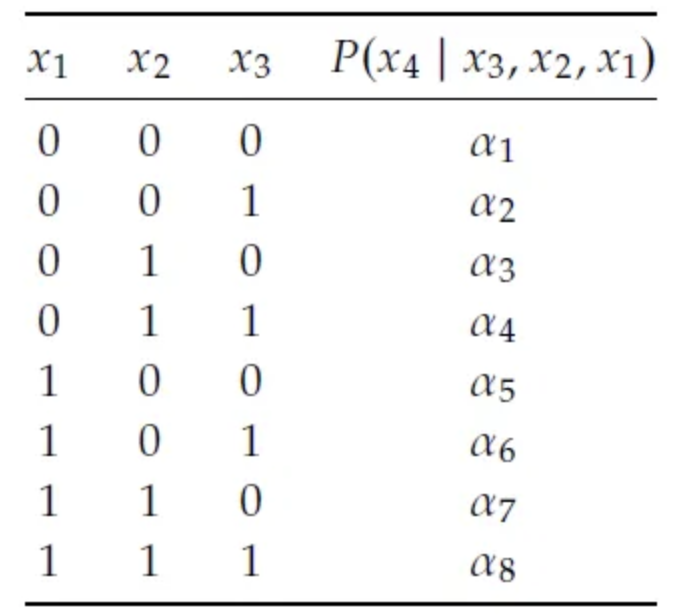
방금 본 문제는 모든 변수가 서로에게 직접 의존한다고 가정한 것과 같기 때문에 나타난다. 그러나 현실에서는 모든 변수가 서로 직접적으로 영향을 주는 것은 아니다. 오히려 대부분의 변수는 일부의 변수와만 직접적인 관계를 가진다. 즉, 변수가 많아질수록, 각각의 변수는 오히려 서로 독립적이거나 조건부 독립적일 가능성이 높다.
만약 우리가 가 이랑만 locally dependent한다는 것을 안다면, 우리는 를 하나하나 계산할 필요가 없다. 만 계산해도 된다. 계산해야 할 파라미터의 수를 확 줄여준다!!
이러한 특성을 반영해 좀 더 효율적으로 모델링하고자 하는 것이 바로 Bayesian Network이다. 이는 변수 간의 관계를 DAG(Directed Acyclic Graph) 로 나타낸다. 그래프에서 한 노드에서 다른 노드로 향하는 엣지는, 그 노드가 다른 노드의 값에 직접적으로 영향을 미친다는 의미를 가진다.
Local Markov Assumption
이때 Bayesian Network가 그래프로 표현된다는 것은 중요한 가정을 하나 내포한다. 바로 Local Markov Assumption(Property) 이다.
Local Markov Assumption
DAG가 주어졌을 때, 각 노드는 자신의 부모(parent) 노드가 given되면, 그래프 상에서 자신의 후손(descendant)이 아닌 다른 모든 노드와 독립이다.
이제 Bayesian Network를 이용해서, 우리는 결합확률분포를 다음과 같이 간단하게 표현할 수 있다.
Bayesian Network Factorization 이라고 한다. (는 의 parent 노드를 의미, 화살표로 딱 한 단계전의 노드들)
예제
간단한 예제를 풀어보자
: 만약 다음과 같이 그래프가 구성되어 있다면, 결합확률분포 는 어떻게 계산할 수 있을까?
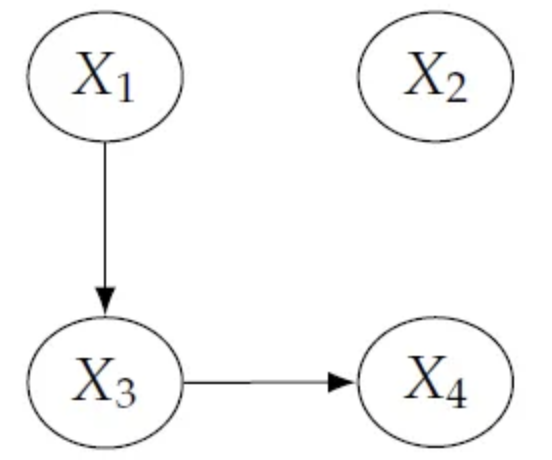
- 답
그런데 이 베이지안 네트워크가 인과 추론에 이용되려면 아직 부족한 점이 있는데… 다음 장에 계속