먼저 3줄 요약부터..
3줄 요약
- 가설 공간이 클수록 알고리즘(머신러닝 모델)이 선택할 수 있는 가설(함수)의 수가 많아진다. 큰 가설 공간은 알고리즘의 높은 분산(variance) 을 유발하여 일반화 성능을 저하시킬 수 있다.
- 모델이 제한된 훈련 데이터로부터 일반화(generalization)를 수행하기 위해 탐색 공간을 제한해주는 설정이 필요하다.
- 내가 귀납적으로 알고 있는 지식 또는 가정을 활용해, 모델에 추가적인 가정을 해서 탐색할 공간을 줄인다. 이것이 Inductive Bias이다.
Inductive Bias
Concept Learning은 탐색 문제로 볼 수도 있다고 했다.
고양이를 완벽하게 구별해낼 수 있는 함수(Target, Concept)가 가설 공간 어딘가에 존재할 텐데… 만약 우리가 찾고 있는 탐색 공간에 그 Target이 없으면, 아무리 많은 데이터를 갖고 지지고 볶아도 실제 함수를 찾을 수 없을 것이다. 훈련 데이터에도 잘 들어맞지 않을 가능성이 크다. (청계천에서 대방어 찾기)
뭐, 그러면 그냥 범위를 엄청나게 넓혀서 모든 가능한 가설을 포함하는 곳에서 탐색하면 되는 거 아니야?
라고 생각했으나,,
이 경우 관찰된(학습) 데이터와 잘 들어맞는 가설(함수)이 너무 많이 생기게 된다. 이 가설들 사이에서 실제 타겟 Concept과 가까운 것을 결정하기가 어렵다.
알고리즘을 사용한다면 하나를 결과로 내놓을 텐데, 이때 이것도 가능하고 저것도 가능하니깐 아무거나 선택한다고 해보자. 그러면 실제 함수를 선택할 가능성은 생겼지만, 반대로 오히려 실제 함수와는 거리가 먼 가설 함수를 선택할 가능성도 높아져버렸다. (모델 분산이 높다)
우리가 원하는 건 우리가 설정한 가설이 새롭게 볼 데이터에 대해서도 잘 일반화(generalization)되어 예측하는 것. 너무 복잡하게 탐색하는 건 그렇게 필요하지 않다.
예를 들어 고양이라는 걸 결정하는데 발톱 유무 같은 건 중요하지 않을 테니까, 이것까지 Input으로 사용하는 함수를 탐색할 필요가 없다. 이것까지 고려하게 되면 오히려 함수의 선택지를 늘려버리는 것이고, 발톱 유무로 고양이 여부를 결정하는 모델의 성능이 좋을 것 같지도 않다. (일반화 성능이 떨어질 수 있다)
그래서 발톱 유무는 고양이 여부를 판단하는데 과감하게(?) 논외로 두기로 한다. 이처럼 우리가 가진 사전 정보 또는 지식을 활용하여 모델에 추가적인 가정을 하고 탐색 공간을 줄이는데, 이것이 Inductive bias이다.
Regression과 Inductive Bias
변수 한 개로 목표를 예측하는 단순선형회귀를 생각해보자. 이를 Inductive bias 관점에서 생각하면, 값이 라는 변수 하나에 의해 선형적으로 분포할 것이라는 추측을 반영한 모델이라고 볼 수 있다. 즉 Intercept, Slope 모수만 찾으면 된다고 탐색공간을 (엄청나게) 제한한 것이다.
실제 를 결정하는 함수가 아래처럼 만 필요하지도 않고, 또 와 비선형적인 관계를 띨 수도 있다. 그건 알 수 없는 일이다.
그러면 우리는 단순선형회귀 모델(가설) ()로는 절대로 실제 함수를 찾을 수 없다.
그러면 최대한 많은 가능성을 고려해서 변수도 여러 개 넣고, 각 변수마다 로그나 Polynomial한 관계까지 고려한 모델을 만드는 것이 좋을까? 실제 함수에 비해 너무 울퉁불퉁한 모델이 만들어질 가능성이 높다.
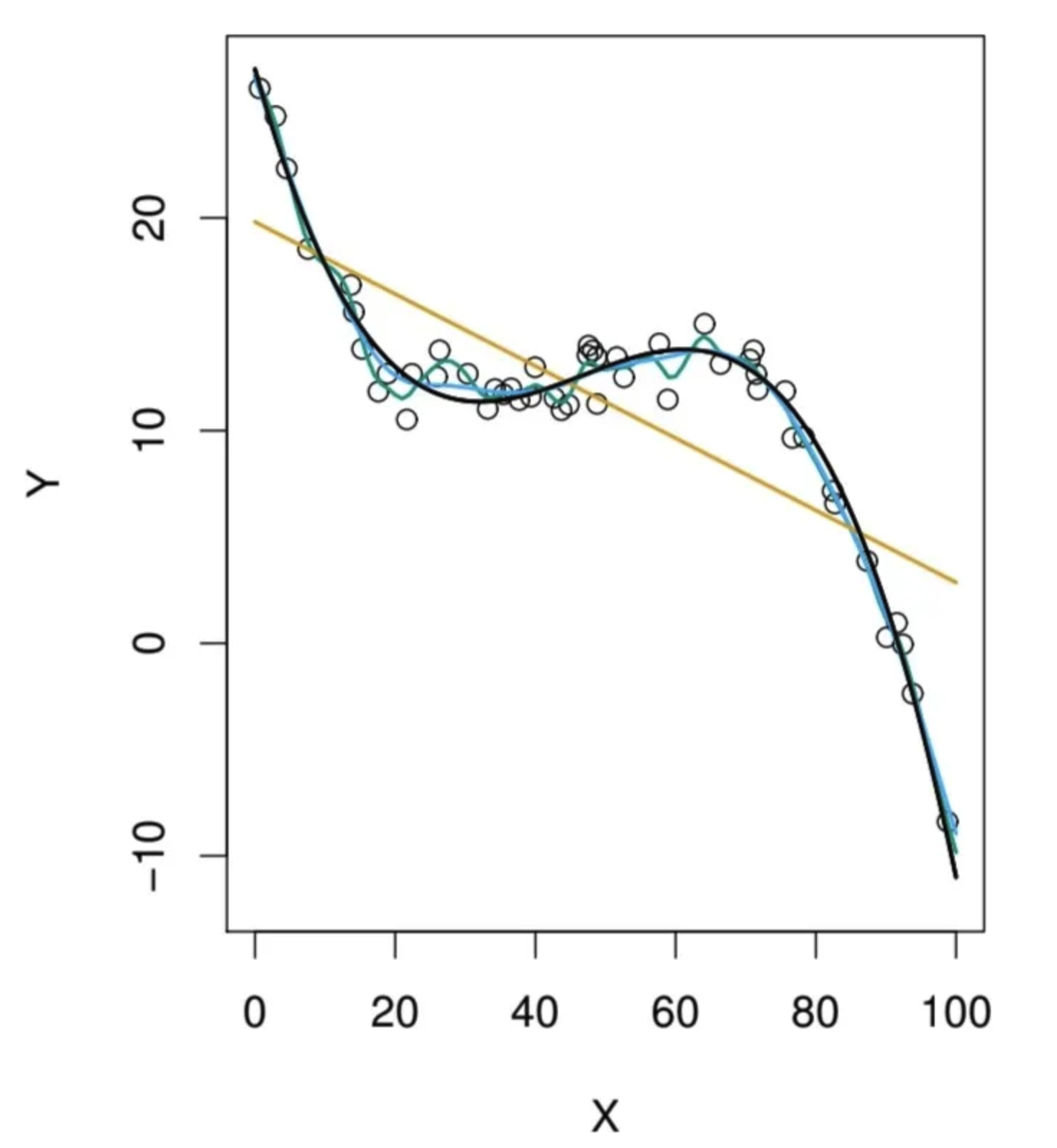
데이터가 분포하는(Y값을 결정하는) 실제 함수가 진한 남색의 선이라고 할 때,
주황색 선이 단순선형회귀로 만들어진 모델, 초록색의 울퉁불퉁한 선이 파라미터를 이것저것 넣어서 만들어진 모델이다. 초록색은 너무 넓은 탐색 공간에서 탐색한 다.
두 개 모두 우리가 원하는 최선은 아닌 것 같다..
즉 우리가 Inductive bias를 잘못 설정해서 탐색 공간이 애초에 잘못되면 실제 함수(Concept)인 에 대해 biased 하게 추정할 것이다. 그렇지만 그만큼 찾는 공간은 작아지기 때문에 분산은 작다.
개인적 소감
실제 데이터를 분석할 때 우리가 생각해볼 수 있는 점은 2가지인 것 같다. 데이터에 따라 얼마나 강한 가정을 모델에 설정할지 결정하고, 데이터를 잘 관찰해서(시각화, 아니면 데이터 자체가 가진 특성을 파악) Inductive bias를 올바르게 설정할 수 있도록 노력하는 것.
예를 들어 CNN은 이미지 데이터에서는 인접한 픽셀들 사이에 의미 있는 연관성 (spatial locality) 이 존재하고, 그 관계가 어디에서든 유지 (positional invariance) 된다는 가설을 반영했다.
Transformer는 Positional Embedding과 Self-Attention을 사용해 모든 정보를 활용한다. 다른 말로 하면 많은 정보를 활용해서 함수의 공간을 넓게 탐색하겠다는 것이므로 Inductive Bias가 약하다.
Local한 정보가 주로 필요한 경우에는 CNN이 좋겠지만, 장면 전체의 맥락같이 Global한 정보가 필요할 경우, 또 데이터가 많은 경우에는 Transformer 모델이 더 유용하게 쓰일 수 있을 것이다.
데이터의 특성과 분석 목적을 잘 이해하고, 적절한 범위 내에서 가설 공간을 제한해 도메인 지식을 활용하여 효율적으로 탐색하는 것이 중요해보인다.